Turinys

• Instrukcijos
• Kaip
• Ką reikia

Suprasti matematinį procesą, susijusį su trapecijos formos skaičiavimu, eina per konceptualios ir praktinės mokslinės konstrukcijos geometrijos širdį. Toliau pateikiamas tekstas yra žingsnis po žingsnio, kad iš pradžių suprastų pagrindinius principus, susijusius su pagrindinės formuluotės lygties kintamaisiais, ir tada naudokite ją trapecinių figūrų problemoms spręsti.

Instrukcijos

Suprasti matematinį procesą, susijusį su trapecijos formos skaičiavimu, eina per konceptualios ir praktinės mokslinės konstrukcijos geometrijos širdį. (matematinis vaizdas pagal jaddingt iš Fotolia.com)

1. Suprasti, kad praktinių projektų, pvz., Gyvenamųjų ar komercinių pastatų, dirvožemio darbų, tokių kaip purvo lovos ir namų vamzdžiai, statyba apima būtinas žinias apie skystų medžiagų kiekį uždaruose vienodo dydžio skaičiumi, o tai leis studentui supratimą apie poreikį apskaičiuoti tūrį. Tikslus esamų matmenų matavimas leidžia tiksliai apskaičiuoti tūrį.

   Trapezoidų, kaip geografinio baseino molio sienų skerspjūvio, paieška praktiškai yra naudinga apibrėžiant trapeciją. Jei dvi keturių pusių figūros pusės yra lygiagrečios, bet nevienodos, o kitos dvi pusės nėra lygiagrečios, šis skaičius vadinamas trapeciniu.

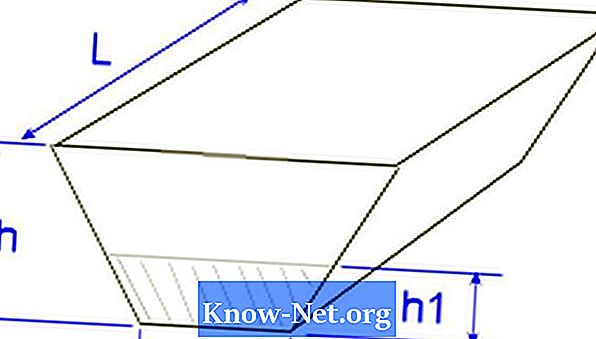
   Taigi, jei turite 22,86 m ilgio figūrą, priekinis matmuo yra 17,37 m pločio ir 10,66 m aukščio, o apačioje yra 21,94 m pločio ir 3,65 m aukščio. aukštis, apskaičiuokite tūrį taip:

   
   

   1. Forma gali būti laikoma 17,37 x 22,86 stačiakampiu priekyje, pritvirtinta prie 21,94 x 3,65 plokštumų apačioje, 22,86 m atstumu;

   2. Tokiu būdu tūrio skaičiavimo formulė, kurią galima nubrėžti kaip kamieną su stačiakampiu viršutiniu ir apatiniu, o ne priekiniu ir galiniu, galima išreikšti kaip V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3, kur kintamuosius galima apibūdinti a1 = 17,37; b1 = 10,66; α 21 D = 21,94; b2 = 3,65; h = 22,86: V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3 V = [17.3710,66 + 21,943,65 + (17,373,65 + 21,9410,66) / 2] * 22,86 / 3 V = [265.60 + (63.54 + 234.11) / 2] * 7,62 V = [265,60 + (297,66) / 2 ] 7,62 V = [414,44] 7,62 V = 3158,03 m³

2. Laikantis formato, trapecijos dinaminis tūris skiriasi nuo statinio modelio, nes statinis trapecijos geometriniu požiūriu yra dvimatė figūra. Skaičiuojamas plotas gali būti tik trapecijos, nubrėžtos dviem matmenimis ant popieriaus. Todėl alternatyvi formulės versija, naudojant vidutinį plotį ir ilgį, yra: V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 Stačiakampyje yra šonų, kurios yra vidutinės viršutinės ir apatinės stačiakampių pusės.

   
   

3. Veikdamas taip, kaip dinamiškas 2 pakopos taikymas, trapecinės konstrukcijos, pvz., Baseino arba uždarojo cilindro, tūris gali būti apskaičiuojamas kaip litrai vienam konkretaus aukščio metrui. Tai reiškia, kad pilno konteinerio tūris, padalytas iš jo aukščio, suteikia tinkamą santykį - naudokite formulę (su matmenimis m), kad gautumėte kubinius metrus.

   Bet kokiam cilindriniam konteineriui, santykis priklausys nuo gylio, jei pageidauja. Ir galima manyti, kad tai reiškia, kad konteineris būtų iš dalies pilnas ir kad tūris būtų nustatomas skirtingais lygiais. Tai reiškia, kad tūris yra aukščio funkcija.

4. Šiek tiek toliau, nes „a“ krypties plotis tiesiškai keičiasi nuo a1 iki a2, a = a1 + (a2-a1) k = (1-k) a1 + ka2; į kuriuos vienetai kh pakyla iš apačios (kur k svyruoja nuo 0 iki 1); tuo pačiu būdu, b = b1 + (b2-b1) k = (1-k) b1 + kb2; kietos medžiagos tūris, kurio aukštis kh, pagrindas a1 b1 ir viršutinis a iki b yra V (k) = [a1b1 + ab + a1b / 2 + ab1 / 2] * kh / 3.

   Jei mes naudojame realų skysčio lygį, o ne k santykį, galime pakeisti k = L / h ir gauti V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L2a2a2b2 + (3Lh-2L2) (a1b2 + a2b1) / 2] * L / (3h ^ 2). Tai suteikia mums apimties kaip gylio funkciją.

5. Tinkamai trapecijos apimties skaičiavimas apima gebėjimą interpretuoti, ar trapecijos figūra yra dvimatė ar trimatė. Dinamiška trapecinio interpretavimo inžinerijos aspekto praktika sukelia tai, ar trapecijos formos figūra yra kažkas, kas yra tiesiog nubrėžta ar sukonstruota, nesvarbu, ar jame yra apimtis, ar paprasta eskizas ant popieriaus.

Kaip

• Geometrinės problemos sprendimas leidžia studentui suprasti, kaip ir kodėl formulė yra taip, ir kodėl aukštis yra toks svarbus kintamasis. Rankiniu būdu gauto atsakymo tikrinimas, pavyzdžiui, naudojant „Hewlett-Packard“ mokslinį skaičiuoklį, yra geras būdas pasiekti visišką tikslumą.

Ką reikia

• Pieštukas
• Užrašų knygelė (su arba be linijų)
• Valdovas